Introduction
This page defines and explains the algorithms that Timekeeper uses to fulfil its central role in the UTC Architecture.
This information may be of interest if you are working on the time system or need a detailed understanding of the internals of UTC on Fuchsia. If you simply wish to develop components on Fuchsia that use UTC, consider reading the much shorter and simpler UTC Overview and UTC Behavior pages instead.
Time source components such as HTTPSDate time source also use a range of protocol-specific algorithms to compute their time samples; refer to the README.md in each time source component for further details.
Overview
The operation of Timekeeper is split into answering seven separate questions:
- Should a time sample be accepted? Each time a sample is received from a time source Timekeeper decides whether it should be accepted (in which case it may lead to a change in the system’s understanding of UTC) or rejected (in which case it is discarded).
- Which time source should be used? Timekeeper maintains a primary UTC estimate that may be influenced by time samples from the Primary, Fallback, or Gating time sources. When more than one of these sources is installed Timekeeper decides which source should be used at each point in time.
- How should a time sample change the estimated UTC? Timekeeper maintains an estimate of the most probable UTC at all times, along with the uncertainty of this estimate. Timekeeper updates both this estimate and the uncertainty each time a sample is accepted from a time source.
- What strategy should be used to converge the reported UTC? Each time the estimated UTC changes as the result of a time sample, Timekeeper chooses how to converge the UTC reported to clients with this new estimate. One option is to immediately step the reported time. Another option is to slew the reported time at some rate for some duration.
- How should a sequence of time samples change the estimated frequency? A sequence of time samples may be used to estimate errors in a device’s oscillator. Correcting for these frequency errors increases the accuracy of the system.
- How can clock error be bounded? The time reported by the UTC clock is unlikely to perfectly match the true UTC. Although the exact error is not known, Timekeeper may estimate and publish a bound on the error.
- What clock updates should be made? Once a convergence strategy has been selected it must be implemented by making one or more updates to the UTC clock object. Estimated frequency and error bound changes should also update the UTC clock object.
In some other time synchronization systems (for example NTP) the same algorithm is used to answer more than one of these questions. This can make it difficult to clearly reason about the behavior of a particular feature, to avoid unintentional interactions between features, or to adjust components of the algorithm in response to new requirements. Timekeeper intentionally uses separate algorithms to answer each question. This leads to a system that is simpler to develop, analyze, and debug and provides greater flexibility to change or reconfigure individual algorithms when supporting a wide range of different products.
The interactions between these algorithms are summarized in Figure 1, where black elements are present in all configurations and grey elements are only present when an optional time source role is present.
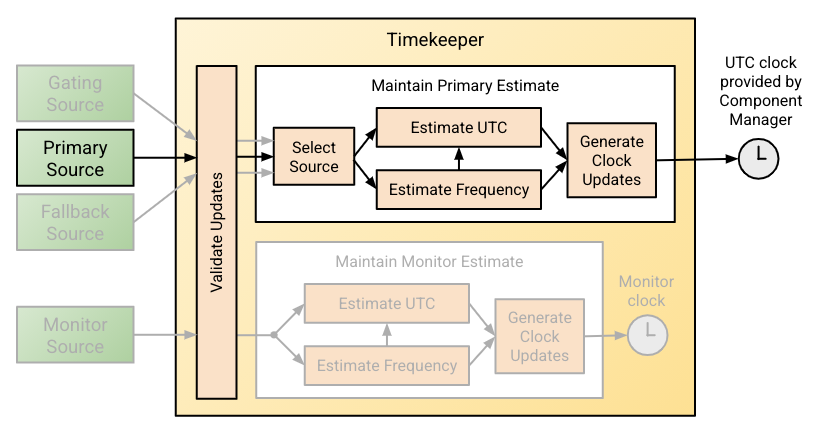
Notation
The following sections sometimes use equations to define portions of the
algorithms. These equations are formatted in code font for ease of
identification and use the following notation:
|x|The absolute value of x.sign(x)The sign of x. Returns -1 if x if negative and +1 if x if zero or positive.sqrt(x)The square root of x.sum(x)The sum of property x over all points within some dataset.clamp(x,y,z)The value x limited to be no less than y and no greater than z, i.e.clamp(x, y, z) = min(z, max(y, x))
Text in UPPER_CASE_SNAKE_CASE refers to configurable parameters that control the behavior of the algorithms. These parameters and their default values are discussed in configurable parameters.
Details
Should a time sample be accepted?
Time samples are subjected to simple validity tests before being accepted:
- Any time sample received less than MIN_SAMPLE_INTERVAL after the previous accepted time sample from the same source is rejected. This limits the maximum resource utilization in Timekeeper as a result of time source bugs.
- Any time sample with a UTC earlier than backstop time is rejected. Accepting a sample before backstop time could cause Timekeeper to place its estimate of UTC earlier than backstop time.
- Any time sample with a monotonic time far from the current monotonic time is an indication of an error. Time samples where monotonic time is in the future or greater than MIN_SAMPLE_INTERVAL in the past will be rejected.
- When Timekeeper is configured with a gating source, any time sample from a
non-gating source where
|sample_utc - (gating_utc + estimated_frequency * (sample_monotonic - gating_monotonic))| > GATING_THRESHOLDis rejected. In this expression gating_utc and gating_monotonic refer to the UTC and monotonic times in the most recently accepted sample from the gating source. This check ensures that all other sources remain consistent with the gating source.
The algorithms designers considered whether to reject time samples that were inconsistent with current estimated UTC (either by being before current UTC or significantly after current UTC) but concluded this was undesirable. Any system that rejects new inputs based on the current estimate is vulnerable to permanent failure if its estimate becomes erroneous and in the case of two mismatched inputs there is no reason to believe the first is more reliable than the second. A system that can recover from an error, even at the cost of a significant jump in time, is preferable to one that cannot.
Which time source should be used?
As introduced in UTC architecture, Timekeeper may be configured to use four different time source roles although it is unlikely that any given product will require more than two.
The primary source, fallback source, and gating source (if these exist) may each be used to drive the primary time estimate and the externally visible clock. These sources are listed in decreasing order of preference; generally a primary time source would be more accurate but less available than a fallback source which in turn would be more accurate but less available than a gating source. A monitor source is subject to consistency checks against a gating source (if one exists) but is otherwise completely independent, driving a separate time estimate and an internal userspace clock that can be compared against the externally visible clock to assess the performance of the monitor time source.
Time sources may take many minutes or hours to converge on an accurate solution so time sources are always launched when Timekeeper is initialized rather than only after the failure of some other time source.
Timekeeper selects the time source based on reported status and the presence of time samples:
- The primary time source is used if its most recent status is healthy and its most recent valid sample was within SOURCE_KEEPALIVE;
- Otherwise, the fallback time source is used if its most recent status is healthy and its most recent valid sample was within SOURCE_KEEPALIVE;
- Otherwise, the gating time source is used if its most recent status is healthy.
Note: As of Q4 2020 gating and fallback sources are not yet supported and therefore the time source selection algorithm has not yet been implemented.
The algorithm designers considered whether to include hysteresis or failure counting in the time source selection algorithm but concluded this would not add sufficient value to compensate for the additional complexity. Many failure modes are accommodated internal to the time sources so complete time source failures should be rare events.
How should a time sample change the estimated UTC?
Each valid sample received from the selected time source should be used to update Timekeeper’s estimate of UTC. Each of these samples contains some error and the size of this error varies between samples. The UTC estimate must therefore combine information from multiple samples rather than blindly following the most recent sample.
This state estimation problem is commonly and efficiently solved using a Kalman filter in other domains. Timekeeper defines a simple two dimensional Kalman filter to maintain the UTC estimate where the two states are UTC time and frequency, expressed as utc nanoseconds per monotonic nanosecond. Note that frequency is maintained external to the filter through the frequency correction algorithm; filter frequency is excluded from the Kalman filter’s measurement model and has a covariance of zero.
The parameters in the Kalman filter are presented in Figure 2.

Note that, as a result of the fixed frequency estimate and the spare process covariance matrix, only the upper left element of the state covariance matrix is ever non-zero. This value is limited to a lower limit of MIN_COVARIANCE to prevent the filter from over-indexing on its internal state and rejecting new inputs.
What strategy should be used to converge the reported UTC?
After each update to the estimated UTC, Timekeeper decides whether to immediately step the userspace clock to the new estimate or apply a rate correction to gradually slew the userspace clock to the new estimate. These options are illustrated in Figure 3.

Step changes in time can be disruptive for time clients and can lead to errors in their calculations so slewing is preferred whenever possible. Slewing is constrained to a maximum rate because slewing at a substantially unrealistic rate could also induce errors in clients; for example, slewing at double real time would be undesirable. Each slew operation is constrained to a maximum duration to bound the time over which the clock is known to be inaccurate; for example, slewing away an error of multiple hours over a period of two weeks would be undesirable.
For small corrections a slew is applied using a fixed small rate for as long as is necessary to achieve the correction. For larger corrections, once the slew duration would reach some maximum, a slew is applied for a fixed duration using whatever rate is necessary to achieve the correction. Once the rate would exceed some maximum Timekeeper resorts to using a time step instead of a slew.
In summary:
- If
|estimated_utc - clock_utc| > MAX_RATE_CORRECTION * MAX_SLEW_DURATION, make a step change to the clock; - Otherwise, if
|estimated_utc - clock_utc| > PREFERRED_RATE_CORRECTION * MAX_SLEW_DURATION, apply a rate correction of(estimated_utc - clock_utc)/MAX_SLEW_DURATIONfor a duration ofMAX_SLEW_DURATION; - Otherwise, apply a rate correction of
sign(estimated_utc - clock_utc) * PREFERRED_RATE_CORRECTIONfor a duration of|estimated_utc - clock_utc|/PREFERRED_RATE_CORRECTION.
How should a sequence of time samples change the estimated frequency?
A device’s oscillator is likely to have some inherent frequency error due to manufacturing imperfections. Estimating the oscillator frequency to account for this error can increase the accuracy of the UTC clock or reduce the frequency at which clock corrections must be made.
The algorithm works with frequency in the form it is applied by the Kalman filter, nanoseconds on the utc clock per nanosecond on the monotonic clock. Note this is the inverse of the oscillator's physical frequency (i.e. nanoseconds on the monotonic clock per nanosecond of real time). An oscillator that is running fast will produce more than one monotonic tick per nanosecond of real time and therefore the UTC clock should run at less than one utc nanosecond per monotonic nanosecond to compensate.
Oscillator errors are bounded by specification to some small value (typically tens of parts per million) hence the UTC estimate algorithm above is stable and reliable even when a frequency estimate is unavailable; the frequency estimate is an enhancement that is beneficial to performance but not necessary.
The frequency estimate is refined over a much longer time period than the UTC estimate. This places the time constants of the two algorithms far apart to avoid potential interactions and ensures the frequency algorithm will not track transient errors such as a temperature driven error while a device is under heavy use. This high time constant means frequency errors would remain in the system for a long time and. As a design philosophy, Timekeeper favors making no improvement in the frequency estimate to introducing an error in the frequency estimate.
Timekeeper estimates a period frequency for each FREQUENCY_ESTIMATION_WINDOW period providing all of the following conditions are met:
- At least FREQUENCY_ESTIMATION_MIN_SAMPLES time samples were accepted during the period. This avoids placing an excessive weight on a small number of samples if time was unavailable for most of the period.
- No step changes in time occurred during the period. A step change is evidence of a significant error either before or after the step. These periods are not used to avoid incorporating this error.
- No part of the period falls within 12 hours of the UTC time at which a leap second may have occurred. Some time sources indulge in leap second smearing where they introduce a significant frequency error for a 24 hour period rather than a step change. These periods are not used to avoid incorporating this frequency error. This affects a maximum of two 24 hour periods a year, fewer if the system tracks whether the next leap second is scheduled.
The period frequency is calculated as the gradient of a least squares linear regression over the (monotonic, utc) tuples for all time samples accepted in the period as illustrated in Figure 4.

This is implemented using the following equation:
period_frequency = {sum(utc * monotonic) - sum(utc)*sum(monotonic)/n}
/ {sum(monotonic^2) - sum(monotonic)^2/n}
Where n is the number of accepted samples within the period. Note that MIN_SAMPLE_INTERVAL places an upper bounds on this value. The overall frequency estimate is calculated as the exponentially weighted moving average (EWMA) of the period frequencies. In all cases the final estimated frequency is constrained to be within double the standard deviation of the oscillator error such that no combination of the events could cause the frequency error to be wildly inaccurate to the point where it could impact the correctness of the Kalman filter. i.e.
estimated_frequency = clamp(
period_frequency * FREQUENCY_ESTIMATION_SMOOTHING +
previous_estimated_frequency * (1 - FREQUENCY_ESTIMATION_SMOOTHING),
1 - 2 * OSCILLATOR_ERROR_SIGMA,
1 + 2 * OSCILLATOR_ERROR_SIGMA)
EWMA provides a simple way to blend data across multiple periods while retaining minimal state.
How can clock error be bounded?
For the UTC clock, the error bound is defined as half of a 95% confidence
interval. In other words, for a randomly selected time on a randomly selected
Fuchsia device, there is a ≥95% probability that the true value of UTC is
between reported_utc - error_bound and reported_utc + error_bound.
Attempting to report any higher level of confidence would imply a level of
certainty that Timekeeper cannot provide because some time failure modes are
invisible to Timekeeper. For example, the local oscillator could be running
outside its specified tolerance due to a defect or a remote time source could
send an incorrect time due to a bug.
The error in the UTC clock is composed of three components:
A known difference between the reported clock time and the Kalman filter UTC estimate while a slew is in progress.
The current clock value and the UTC estimate are easily calculated at any point therefore calculating the difference is trivial. The error bound includes the complete difference, however, this is overly pessimistic.
An unknown difference between the Kalman filter UTC estimate and the time standard used by the remote time source.
Each time source supplies error standard deviations with its time samples. The probability distribution of these errors is not known and may differ between time sources. However, based on the central limit theorem, the normalized sum of independent random variables approaches a normal distribution even if the original random variables were not normally distributed. Since the Kalman filter is averaging the input samples (albeit not equally), it is expected that the error distribution of the Kalman filter approaches a normal distribution as the filter accumulates a large number of samples, with a standard deviation that is determined by the covariance. This error bound includes a term of twice the square root of covariance in the error bound to account for this error component. This this may either be optimistic or pessimistic for early time samples while the filter error is dominated by the unknown probability distribution received from the time source.
A known difference between the time standard used by the remote time source and true UTC.
Some sources, such as Google, "smear" leap seconds by deliberately introducing an error of up to 500ms to the reported time during the 24 hours surrounding a leap second. This algorithm does not document this error in the error bound, reasoning that the complexity and computational cost of documenting smearing error is not worth the benefit to time clients. Leap seconds occurred five times between 2000 and 2020 causing a smearing error on 0.07% of all days in this range. It is unlikely this can cause the final bound to fail the 95% confidence criteria.
In summary, the error bound is calculated in the following way:
error_bound = 2 * sqrt(covariance[0,0]) + |estimated_utc - clock_utc|
Until the Kalman filter has been initialized by receipt of the first time
sample, the error bound is set to ZX_CLOCK_UNKNOWN_ERROR. This includes the
case where the clock has been initialized from the real-time clock (RTC) but the
network time is not yet available.
The error bound calculation is summarized in Figure 5:
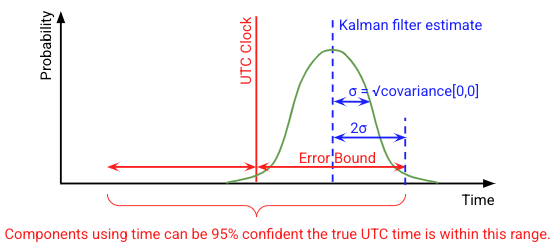
What clock updates should be made?
Changes to the rate and offset of the clock follow directly from selecting a convergence strategy and estimating the oscillator frequency as discussed in earlier algorithms. The error bound defined by the previous algorithm is a continuously changing value that must be periodically published in the clock.
While a large slew is in progress the clock is continually approaching the
Kalman filter estimate and therefore the error bound is continuously decreasing.
To limit resource utilization Timekeeper only updates
zx_clock_details_v1.error_bound during a slew when either some other clock
update is required or when the error in the last reported value exceeds
ERROR_BOUND_UPDATE.
While a slew is not in progress, the error bound is continuously and slowly
increasing as the oscillator frequency error accumulates. Outside a slew,
timekeeper updates zx_clock_details_v1.error_bound at some conveniently low
frequency, ensuring that the error in the last reported value never exceeds
ERROR_BOUND_UPDATE.
In summary, Timekeeper makes updates to the UTC clock as follows:
- Step changes to the clock are always implemented as a single clock update.
- Clock slews are usually implemented as two clock updates: a rate change to
1/estimated_frequency + rate_correctionwhen the slew is started followed by a rate change to1/estimated_frequencyafter a delay ofslew_duration. If a subsequent update is accepted before this second clock change, the second clock change is discarded. - If a new frequency estimate is calculated while no clock slew is in progress,
the clock rate is changed to
1/estimated_frequency(if a clock slew is in progress, the clock update at the end of the slew picks up the new frequency update). - If
|last_set_error_bound - error_bound| > ERROR_BOUND_UPDATE, the error bound is updated.
Configurable Parameters
The previous sections introduced a number of parameters that may be used to configure the behavior of the algorithms. The following tables provide more information about each of these parameters and justify the initial value that is used.
GATING_THRESHOLD
The gating threshold limits how close time samples from non-gating sources must be to the UTC that the gating source indicates. This may be used to ensure less trusted sources are broadly consistent with a cryptographically verifiable time source.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | Not Yet Implemented | Not Yet Implemented |
MIN_SAMPLE_INTERVAL
The minimum sample interval bounds the maximum rate at which Timekeeper is
willing to accept new samples from a time source in order to limit the
Timekeeper resource utilization. Note this is relevant since in the
fuchsia.time.external.PushSource protocol it is the time source that
determines when time samples should be generated. This value is also used to
apply an upper limit on the monotonic age of time samples.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | 60,000,000,000 (i.e. 1 minute) | In general we expect time sources to reduce the frequency of time samples as they converge on an accurate time, with time samples in a well calibrated system arriving tens of minutes apart. Accepting a sample every minute is much faster than the rate needed after convergence and roughly reflects the fastest rate we expect shortly after initialization. Processing one time sample per minute per time source would still mean Timekeeper was using a very small fraction of the overall resources and was not frequently spamming the log. |
SOURCE_KEEPALIVE
The source keepalive determines how frequently a source that declares itself to be healthy needs to produce samples in order to remain selected. If a time source fails to generate any time samples for this period and a source lower in the primary > fallback > gating hierarchy is available that other source will be used instead. This parameter is not used unless either a fallback or gating time source is configured.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | 3600,000,000,000 (i.e. 1 hour) | Time sources should mark themselves as unhealthy when there is some persistent reason they cannot supply time. This parameter should be viewed as a last resort that enables recovery in the event of time source lifecycle bugs. We pick a value that is longer than we expect the slowest time source will use for samples while healthy (and in doing so place a minimum rate requirement on time sources), but short enough that the system clock will not have diverged significantly by the time the error is detected. Over one hour a 25ppm oscillator might have diverged by 90ms, hence we use this as a reasonable initial value. |
OSCILLATOR_ERROR_SIGMA
The standard deviation of the system oscillator frequency error, used to control the growth in uncertainty during the prediction phase of the Kalman filter.
| Units | Value | Rationale |
|---|---|---|
| Dimensionless | 0.000015 (i.e. 15 ppm) | Eventually this should be configurable per board to reflect the hardware specification. For now we default to a value that is typical for low end consumer hardware. |
MIN_COVARIANCE
Minimum covariance bounds the minimum uncertainty of the UTC estimate in the Kalman filter. This helps the filter not drink its own bathwater after receiving very low uncertainty samples from a time source.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds squared | 1e12 (i.e. 1e-6 s^2) | This value represents a post-correction standard deviation of one millisecond. This value is lower than the filter achieves naturally with network time sources and therefore does not often come into play. If very high accuracy time sources such as GPS were used in the future it may be appropriate to lower the value somewhat. |
MAX_RATE_CORRECTION
Max rate correction bounds the fastest rate at which Timekeeper will deliberately adjust the clock frequency in order to slew away a UTC error. This is in addition to any clock frequency adjustment used to compensate for an oscillator frequency error.
| Units | Value | Rationale |
|---|---|---|
| Dimensionless | 0.0002 (i.e. 200ppm) | 200ppm represents approximately one order of magnitude above the error rate that could be expected from a typical oscillator error. We believe this magnitude should be accommodated correctly by most clients and it is comfortably within the 1000ppm limit imposed by the kernel. When combined with MAX_SLEW_DURATION this value ensures a 1 second error may be removed by slewing. This is desirable to elegantly handle leap seconds and potential artifacts from time sources that only receive integer seconds. |
MAX_SLEW_DURATION
Max slew duration bounds the longest duration for which Timekeeper will apply a clock frequency adjustment in response to a single time sample. Consecutive time samples may introduce errors that each trigger a slew and therefore this per-sample duration does not constrain the total time over which Timekeeper may be in the process of slewing.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | 5400,000,000,000 (i.e. 1.5 hours) | The typical interval between time samples is tens of minutes. A 90 minute maximum implies a correction received in one time sample may result in a slew that spans the next handful of samples (each of these samples could also cause a modification of the slew), which feels appropriate. 90 minutes is long enough to achieve meaningful time corrections but short enough that any user-visible abnormalities associated with a slew or time error are not present over multiple hours. When combined with MAX_RATE_CORRECTION this value ensures a 1 second error may be removed by slewing. This is desirable to elegantly handle leap seconds and potential artifacts from time sources that only receive integer seconds. |
PREFERRED_RATE_CORRECTION
The rate at while Timekeeper adjusts the clock frequency to slew away small errors.This is in addition to any clock frequency adjustment used to compensate for an oscillator frequency error.
| Units | Value | Rationale |
|---|---|---|
| Dimensionless | 0.00002 (i.e. 20ppm) | 20ppm is consistent with the error that might be observed from a typical oscillator and therefore must be accommodated by all time clients; there is little value in using a lower rate. 20ppm is high enough to correct typical moderate errors in a handful of minutes - a 10ms error would take 50 seconds to remove. |
FREQUENCY_ESTIMATION_WINDOW
The time period over which a set of time samples are collected to update the frequency estimate.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | 86,400,000,000,000 (i.e. 24 hours) | The value should be a multiple of 24 hours to avoid a bias from different temperatures in the diurnal cycle. Longer periods would lead to more opportunities to exclude or fail to complete a time period and therefore a less reliable frequency estimation process. 24 hours provides a sufficiently large number of samples to average and is sufficiently distant from the time constants in UTC estimation. |
FREQUENCY_ESTIMATION_MIN_SAMPLES
The minimum number of samples that must be received in a frequency estimation window for it to be eligible for a frequency estimate.
| Units | Value | Rationale |
|---|---|---|
| Dimensionless | 12 | SOURCE_KEEPALIVE and FREQUENCY_ESTIMATION_WINDOW bound the minimum number of expected time samples to 24 for a device whose time source was healthy for the entire window. We require that half this number be received, meaning a device operating at the slowest legal sample rate must be online for half of the 24 hour window. This value ensures that each time sample has a limited contribution to the final average and therefore a small number of outliers may be accommodated. |
FREQUENCY_ESTIMATION_SMOOTHING
The factor applied to the current period during the exponentially weighted moving average calculation of frequency.
| Units | Value | Rationale |
|---|---|---|
| Dimensionless | 0.25 | 0.25 sets a moderate (and somewhat arbitrary) bias towards the history during the EWMA calculation, with the historic frequency being weighted three times higher than the current period frequency. This damps the impact of any abnormal frequency periods and encourages a stable long term average. |
ERROR_BOUND_UPDATE
The minimum change in value that causes the error bound in UTC clock details to be updated even when no rate or offset changes are required. This parameter controls how frequently the clock must be updated while a significant slew is in progress.
| Units | Value | Rationale |
|---|---|---|
| Nanoseconds | 100,000,000 (i.e. 100ms) | An error bound update of 100ms combined with an error bound growth of 30ppm from OSCILLATOR_ERROR_SIGMA means one error bound correction is required every 10 minutes during a maximum rate slew. This seems to be an appropriately low burden to maintain error bounds. |
